NATO Standard Sights

NATO Standard Sights

In NATO (North Atlantic Treaty Organization) a standardization agreement defines common standards and specifications between the member countries for equipment and procedures. This provides a common standard for equipment and set of expectations to ensure military personnel can operate NATO equipment with some degree of interchangeability across military services on similar types of vehicles. In practice, there is still some degree of variation. NATO Standard Sights are sights that adhere to a common measurement, in this case mils, and put markings on the sighting reticules which are used to measure distance of targeted objects as well as provide lead where required. What are Mils? A mil, an approximation of milliradians (mrad), is a unit of angular measurement commonly used in firearm and armament optics as a frame of reference to ensure accuracy over distance. NATO (because we are talking about NATO standard sights, after all) defined dividing a circle into 6400 mil, while other countries sometimes use 6280 or 6300. For purposes of range estimation, this difference is negligible. 6400 works better for calculations done in your head.

In a tank or other fighting vehicle, the GPS (Gunner Primary Sight) reticule provides the aiming reference for engaging targets using a fire control system solution. It is marked in mils to also assist in range and manual lead determination.

Example: M1A1 Gunner Primary Sight Reticule Markings Measured in MILS

The secondary function of reticule is to sanity-check results from a rangefinder to make sure it is operating properly and not reflecting a much closer objects range, such as the nearby ground or a passing obstacle (tree, bird, another vehicle) between the sight operator and the target.

The markings on a sighting reticule are used by providing an easy-to-remember and apply frame of reference for how large an object at a certain distance should appear next to those reticule markings. For example, in the simplified diagram below, a 2.2m-tall and 3.8m-wide tank should fit across one measurement at 1km, and the tank may take up approximately the same space when its 7.5m long hull is viewed broadside at a 2km distance. 7.5m is almost twice 3.8m, so something 3.8m-wide at 1km would need to be around 7.5m-wide at 2km to take up the same amount of space on a reticule marking used to measure that range. The diagram below demonstrates this concept:

Two tanks at different ranges occupying the same space in mils when viewed through a sighting reticule

So using this same principle, on an M1A1, you can use the reticule markings in absence of a laser ranging system to estimate the distance of a tank whose dimensions you roughly know.

The important measurements are not just height, but length and width of hull. The longest measurement you can compare against the reticule means a lower total error measurement. For instance, a 7m-long hull measured on the reticule reduces the error vs. a smaller height or width, assuming that the measurement accuracy is always the same (say, a quarter of a mil). All else being equal, the larger the known dimension you can compare with reticule markings, the better your accuracy (or conversely, the smaller the significance of the error).

As the prospective gunner of a tank, you may want to memorize the dimensions of the vehicles you are most likely to encounter. This will allow you to generate range estimates in the greatest number of potential scenarios, such as if a vehicle is partially obscured or in oblique aspect.
A good summary of these vehicles is available here.
To demonstrate this concept, we will use a T-90A as an example, which has these measurements:
Height: 2.22 meters (rounded to 2.2 in the calculations below)
Width: 3.78 meters (rounded to 3.8 in the calculations below)
Length (hull): 7.5 meters

Note that the above may vary depending on which source you reference, but for the purposes of this tutorial, we will be going with these figures, which align with what is simulated in Steel Beasts.
In this example, a T-90A, which is about 2.22m-tall, almost just slightly pokes above when put between the first reticule markings above and below the center circle of the GPS when it is 1 km away. Note that the distance between these two reticule markings is 2 mils, so this would align well with the expectation that an object 2.22m tall would protrude by another quarter of a mil. Looking horizontally, the 3.78m-wide tank takes up all of the first marking, which is 2 mils, and about 70% of the second, which is 2.5 mils (so 0.7 X 2.5 = 1.75 mils), for a total of 3.75 mils of horizontal space, which we can round to 3.8.
So: 3.8m-wide / 3.8 mils-wide = 1000m.

However, had the T-90 fit almost exactly between the two vertical marks, this would mean a 2.2m-tall object was taking up 2 mils of vertical space on the reticule, putting it at 2.2m/2 mils = 1100m, significantly farther, demonstrated below:

From the left side of the first reticule marking outside of the center circle on the reticule to the middle of the second two markings is 3.5m, as the first line from the center is 2 mils, the second, 2.5, for a total length of 4.5. In the image above, the T-90 is taking up all of the centermost marking (2 mils), and half of the second (so 0.5 X 2.5 = 1.25), for a total of 3.25 mils of horizontal space. A T-90, which is 3.8m wide, taking up 3.25 mils of space, would be: 3.78/3.25 = 1,163m away, so perhaps this is the more accurate range estimate give. Note that in the screenshot above, it is easier to see the width difference than the height difference, a clue that larger measurements are more reliable for these kinds of estimates.
As a counter-example, if instead the target vehicle had been a T-80, which is 3.5m-wide, seeing it take up the same amount of space, like the below…

…would mean that a 3.5m object is taking up 3.75 mils worth of space, so 3.5/3.75 = 933m, significantly closer, and something to be accounted for when firing based on reticule markings instead of a rangefinding system. If it is daunting to calculate figures like this, try instead to think of it as 14/4 divided by 15/4, which is really the same as 14/15 when simplified.
If you don’t recognize the target or haven’t memorized its dimensions, using 3.5m hull width is a useful rule of thumb as most military vehicles are constrained by railway loading limits.
In the case of profile view, you are given the opportunity to compare the longer hull measurement against the reticule markings to make an estimate. Consider the example below, a profile view of a T-90, which has a 7.5m-long hull. As you can see below, the hull, from the beginning of the first reticule marking from the center until the right side of the second horizontal reticule is 4.5 mils (2 mils + 2.5 mils).
7.5m hull / 4.5 mils of horizontal space = 1667m (75/45 or 5/3)

Note that we could sanity-check this estimate by using the 2.22m height vs. the 2 mil distance between the two reticule markings that straddle it vertically. From the image above, the height is about 70% of the distance between those two points, so:
2.2m / (70% X 2 mils = 1.4 mils) = 1571m (or 22/14)
Note the volatility of a shorter measurement when making estimates – This will be a topic we revisit later, but it is worth noting now how just a minute change can vastly skew the estimate when using smaller numbers on both sides of the division.
Example, if we decide the vertical space is instead 1.5 mils (so 75% of 2 mils in vertical space), the equation becomes:
2.2m / (75% X 2 mils = 1.5 mils) = 1467m (or 22/15)
What we have demonstrated so far is something called the WERM formula.

The WERM Formula

The WERM formula is a way to use the reticule marks of a sight to generate a more precise distance estimate, using the same logic we already applied above.
The WERM formula is short for:
Width = (Equals) Range X Mils
In this case, because we want to know the range, but presumably know the Width (or Height) of the object (approximately), we can use algebra to rewrite the equation to:
Range (in thousands of meters, or km) = Width (or Height) in meters / Mils (as measured on a sighting reticule)
Suppose in a combat situation vs. a T-90 we did not know the range of that enemy vehicle – perhaps the rangefinder disabled (or nonexistent). As we mentioned earlier, we know that a T-90 is about 2.22m-tall (rounded to 2.2 for practical calculations), and 7.5m-long. In the real world, we are seldom presented with perfect head-on or profile aspect views of the target, and that is the case here. The target vehicle is partially obscured, and at an angle and slope that prevents accurate length estimates. So what to do? Well, we can at least see fairly unobstructed view of the height, and compare it with the sight markings adjacent to it. In this case, we know the vertical distance between the inner-most marking and the second pair is 1 mil, and the T-90 spans about 90% of that distance.
2.2m-tall / (0.9 mils vertical space) = 2444 meters (Or 22/9)
In reality, this target was 2450 meters away, so a fairly close estimate and small margin of error. Having the extra magnification on the M1A2 thermal sight helped bring a more accurate estimate, but that is not always available.

In this situation below, the thermal sight is out of order, and we are looking at another tank type this time, the T-72. A T-72 is 7 meters long and 2.3 meters high. This tank is slightly more in profile than our last example, but looks a bit small in our sights. Understandably, we will do what we can to get an accurate distance under the limitations of our equipment and the situation. Comparing the length, it looks like 7 meters taking up 2.75 mils of horizontal space on the reticule.
So:

7m-wide / 2.75 mils = 2545 meters

In reality, this target was 2670 meters away.

Finally, for an example where information is extremely limited, consider the below, where a T-72 turret is barely poking above the contour of the hill.

In this case you can either try to use the known width of the turret (2.6m) or the height of the turret (0.8m) to get a reasonable estimate. The center square of the M1A2 reticule is 1 mil in diameter (or 0.5 mils in radius to either side of the center dot), and the turret looks to be slightly wider – let’s call it 1.2 mils.
So:
2.6m wide / 1.2 mils (or 26/12) = 2166 m.
Or a 0.8m tall turret taking up about .4 mils vertically = 0.8m/0.4 mils, simplified to 8/4 = 2000m.
And if you thought the turret was taking up closer to half of the vertical space (so 0.5 mils), the range estimate changes to 1,667 (8/5), which demonstrates again how sensitive the equation is when used on smaller measurements vs. larger ones to narrow the margin of error. That is a wide range (1667-2166m), but sometimes that is the reality of working with limited information. In situations like these, picking what is probably the right range based on the longer known measurement is the best path.
The actual range shown here was 2050 on the rangefinder. All three estimates were straddling this reality, but the one derived from the longer known measurement, the 2.6m turret width, provided us a more accurate estimate compared to reality and is less sensitive to minor differences in estimating the measurements in mils.

Leopard 1 and 2 Gunner Primary Sights

Within NATO, different armored vehicles vary across how reticule markings are laid out and what mil measurements are in place.
For example, the Leopard 1 and 2 GPS reticule has a different configuration from the US Abrams family of tanks. For example, on the US reticule, the center circle measures 1 mil in diameter, while the Leopard reticule is 0.5 mils, representing the dispersion of the laser beam cone on the rangefinder. The US reticule loses some of that detail in favor of attempting to provide visibility at the center of that aim point and is 1 mil in diameter.

Example: L2A5 Gunner Primary Sight Reticule Markings Measured in MILS

T-64 Innovations to Disrupt Visual Range-Finding

As a historical note on the importance of using reticule markings for ranging purposes, one of the innovations the Soviets introduced into the T-64 was the ability to open side gills to alter the perceived width of the vehicle, creating the illusion of up to an extra meter of width. For sights that relied on known width values to estimate range, this could throw off the firing solution and lower the resulting chances of hitting on a first shot exchange long enough to create an advantage to T-64 crews. While this became a moot point with the introduction of laser-range finding, it is still important in any application where firing solutions rely on purely visual references, such as historical scenarios in Steel Beasts set before the mid-1970s, or scenarios simulating armed forces in the present that rely on technology from that period. Examples of this are developing nations or factions in a civil war that are limited in terms of the equipment they can acquire, and as a result use recovered or captured equipment considered second-hand or obsolete by more affluent or well-connected armed forces.

To demonstrate this concept, we have created a scenario using a Sho’t Kal tank, a contemporary of the T-64. The Sho’t Kal tank was the result of re-arming the British Centurion with a L7 105mm tank, and the vehicle entered service in 1970, seeing service in the Yom Kippur War and subsequent fighting in Lebanon in the 1970s and 1980s.
The Steel Beasts wiki entry on the Sho’t Kal can be found here, and the vehicle is fully playable in Steel Beasts. In the scenario linked here, we are creating a situation with low visibility where the gunner needs to rely on visual ranging reticule markings to successfully engage T-64A tanks in low-visibility, daylight conditions.
To assist with this process, we are providing the following quick references on the Sho’t Kal gunner’s primary sight, with additional info referencing a practical application of the WERM formula to help successfully engage these targets.
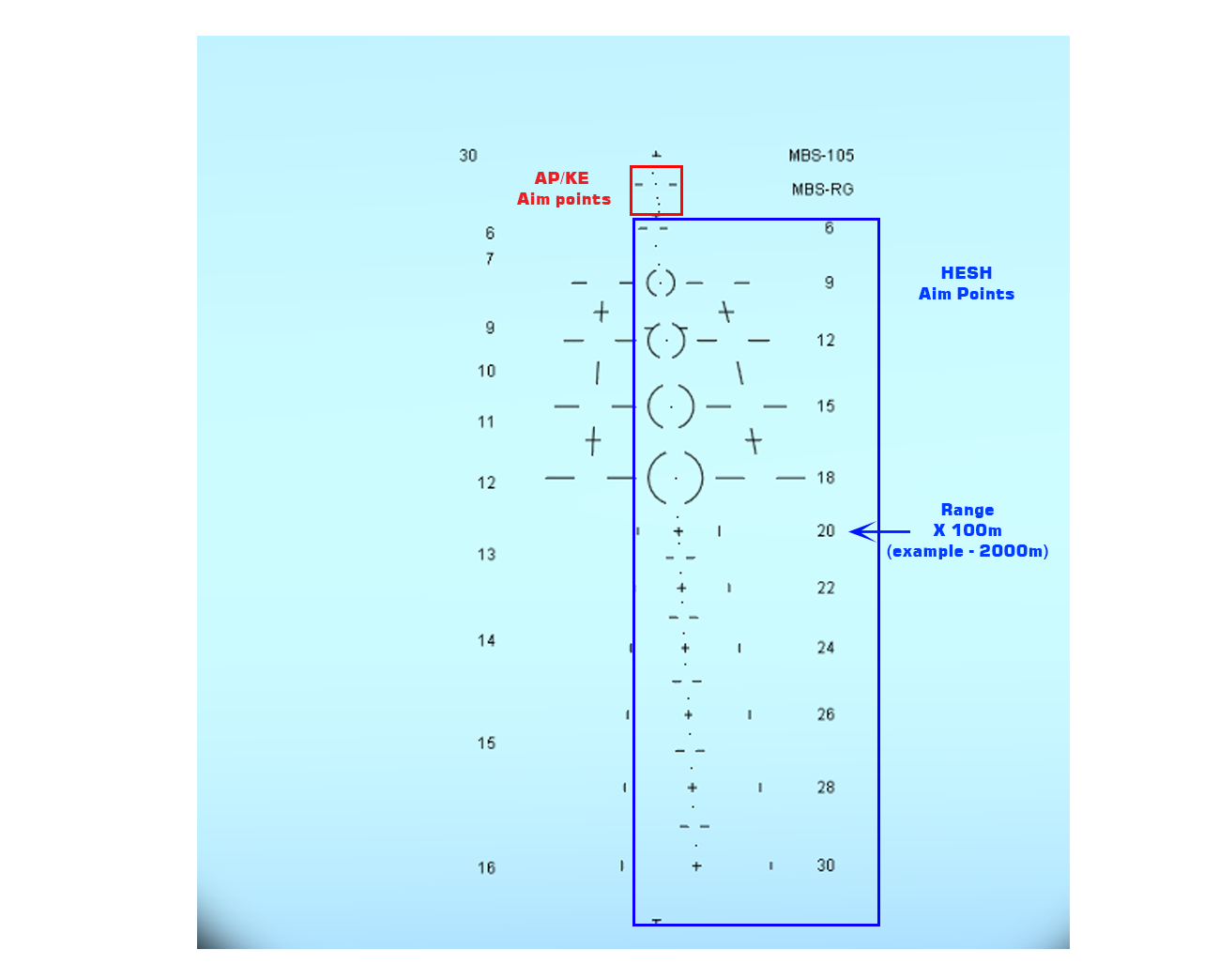
First, the diagram below explains what part of the reticule is relevant for which ammo type – AP/KE (Armor Piercing/Kinetic Energy) rounds, or HESH (High Explosive Squash Head), which for our purposes, have a similar ballistic profile to HEAT rounds (though a different impact mechanism).

This diagram shows the drastically different hold-over necessary when using the Sho’t Kal GPS for each ammunition type. The AP/KE rounds have a relatively flat ballistic profile, while the HESH rounds require a higher arc, and have a longer flight-time as well, which makes it more difficult to hit a moving target. The HESH reticule markings have clear markings on the right side of the GPS to show which dot you should be using to aim those rounds.

Because the AP/KE aimpoints are more compressed, we have provided a zoomed view of these with the relevant distances called out below.

With this in mind, we now approach the topic of how to use a concept like WERM to estimate targets on a primary sight that does not have an explicit ranging scale, but needs some rule of thumb to estimate target distances to use properly.
Note the dimensions of the T-64 below, and compare/contrast it with the T-55:

The dimensions are almost identical, other than the T-55 is 10 centimeters taller. Additionally, as mentioned earlier, the gill flaps on the T-64 can create the illusion of this vehicle being almost a meter wider, which could then lead to the commander of an opposing vehicle assuming it is closer than it appears, especially in low-light conditions.
So how does one use the Sho’t Kal gunner’s primary sights to estimate distance? Below are some suggested, though unofficial, techniques to do so using known ranges to provide a sight picture and some basic logic to use on the scenario we have created to practice these skills.

At 500m, the T-64 fits just inside the top and bottom cross the bracket the AP/KE aimpoints. Frankly, at this range the AP/KE is going to hit at or slightly above the 800m aimpoint, so this is a good clue you will not have to adjust at all to hit your target with that ammunition, while with the HESH rounds, you will be using the bottom cross, right above the 600m aimpoint.
This tells us the distance between the top and bottom cross is about 4.4 Mils:
2.2m-tall tank / 500m (0.5km) = 4.4 Mils.

At 1km (1000 meters), the same T-64 fits almost exactly between the top cross and the first set of twin in-line reticule markings at the top of the reticule. This means the distance between those two sets of points is about 2 Mils :
2.2m-tall tank / 1km = 2.2 Mils

Finally, at 2km, which is at the edge or slightly beyond our existing aimpoints for AP/KE, but still within effective engagement distance for HESH on static targets, we have two different ways we can verify the range of the target. First, at head-on aspect, and at profile aspect, the T-64’s hull height is almost exactly the distance from the both top dual reticule markings that are below the second cross, and just above the second cross. This means the space between those markings is about 1 mils total vertical length:
2.2m-tall tank / 2 km = 1.1 Mils.
Second, at profile aspect, the T-64’s hull is almost exactly the distance from the outer ends of both top reticule markings that are below the top cross. This means those reticule markings are about 3.25 mils total horizontal length:
6.5m-long tank / 2km = 3.25 Mils.
To summarize, here are the approximate mils markings to use for WERM calculations using the Sho’t Kal sight:

Now it is time to put your WERM and visual ranging skill to the test. We have provided a scenario here that pits you against a major push by multiple platoons of T-64 and T-55 tanks, in rainy weather and early evening light conditions. As you can see, when visibility is limited by rain and low-light conditions, those gill flaps can make a significant difference on range estimates.
Here is a T-64 with gill flaps out at in overcast weather and light rain at 1540m:

Here is a T-64 without gill flaps in the same conditions and at the same range:

As you can see, the only real discernable difference is that the T-64 with gill flaps looks closer due to the perceived width. The gill flaps add enough false width that it would be easy to think the T-64 with gills extended looks closer to 1166m than 1540 (visually, taking up about 3 mils, so 3.5/3 = 1166m). You can see how at these ranges, it is almost impossible to discern the difference between a tank using gill flaps and not, and it does make a visual difference for perceived width and thus range. This is the extra 100-300 meters of ranging uncertainty that can make the difference between a first-exchange hit or miss. Experience this challenge in our scenario and see what it takes to do tank gunnery the hard way!

Sources:

https://en.wikipedia.org/wiki/Standardization_Agreement
https://apps.dtic.mil/dtic/tr/fulltext/u2/a156802.pdf
https://en.wikipedia.org/wiki/Milliradian
https://en.wikipedia.org/wiki/Sho%27t
https://www.steelbeasts.com/sbwiki/index.php?title=Range_Estimation